VISIT STATE HEALTH COMPARE
Blog & News
Research Assistant
What Are Statistical Tests? Statistical Testing and How to Determine Statistical Significance — A SHADAC Basics Blog
September 06, 2024:
Basics Blog Introduction
SHADAC has created a series of “Basics Blogs” to familiarize readers with common terms, concepts, and topics that are frequently covered.
This Basics Blog will focus on the topic of statistical tests & testing—including what statistical testing is, how to do a statistical test (specifically, how to do a t test), related definitions, and how to interpret statistical significance, within the context of data drawn from SHADAC’s State Health Compare.
Keep reading below to learn more about statistical testing and statistical significance.
What Is Statistical Testing?
Statistical testing can tell us if there is enough evidence to determine if an estimate is statistically different from another estimate, within a certain level of confidence.
There are various types of statistical tests that are used in different situations. The test used depends on the type of data, variable types, data distribution, and other factors. Some examples of statistical tests include:
- T-Test
- Z-Test
- ANOVA test
Researchers at SHADAC most often use a “T-Test ” to test for significance in our research and analysis. T-tests are typically used to compare the means or percentages of two independent populations.
Definitions
To get a better understanding of statistical testing and its meaning in data-driven research, we will walk through an example, using a t-test. Then, we can determine statistical significance from the results of the t-test, which we will explain later in this blog. Before that, however, we will need to define some related terms and values that are used in the t-test formula.
The following formula is used to conduct t-tests:
Let’s break down this formula and look at the definitions of each of its parts:
Statistical Estimates: approximation of an unknown true population (ex: a sample).
Statistical estimates are the “best guess” of a true population.
Difference in Estimates: the mathematical difference between the statistical estimates (estimate 1 – estimate 2).
In a t-test, estimates are typically a percentage or mean.
Standard Error (SE): estimate of the (un)certainty and precision of a given estimate.
Smaller standard error = less uncertainty, greater precision
Larger standard error = more uncertainty, less precision
T-Critical Value: a value that is the threshold for significance.
T-critical values are set based on what confidence interval is being used. 1.96 is the t-critical value for tests using a 95% confidence interval, which is commonly used.
T-Statistic Value: used to determine whether a value is significant or not
The t-statistic value is compared to the t-critical value to determine significance.
Margin of Error (MOE): within a specified confidence interval expresses that the true population lies within a range of the provided estimate.
The smaller the margin of error, the greater the precision of the estimate.
Confidence Interval: expresses the interval in which we expect the true population value to fall at a given level of certainty.
The greater the confidence interval (ex: 99% compared to 95%), the greater the certainty. For example, we could say we are 95% confident that a value is significant.
How to Do a T-Test: Using State Health Compare
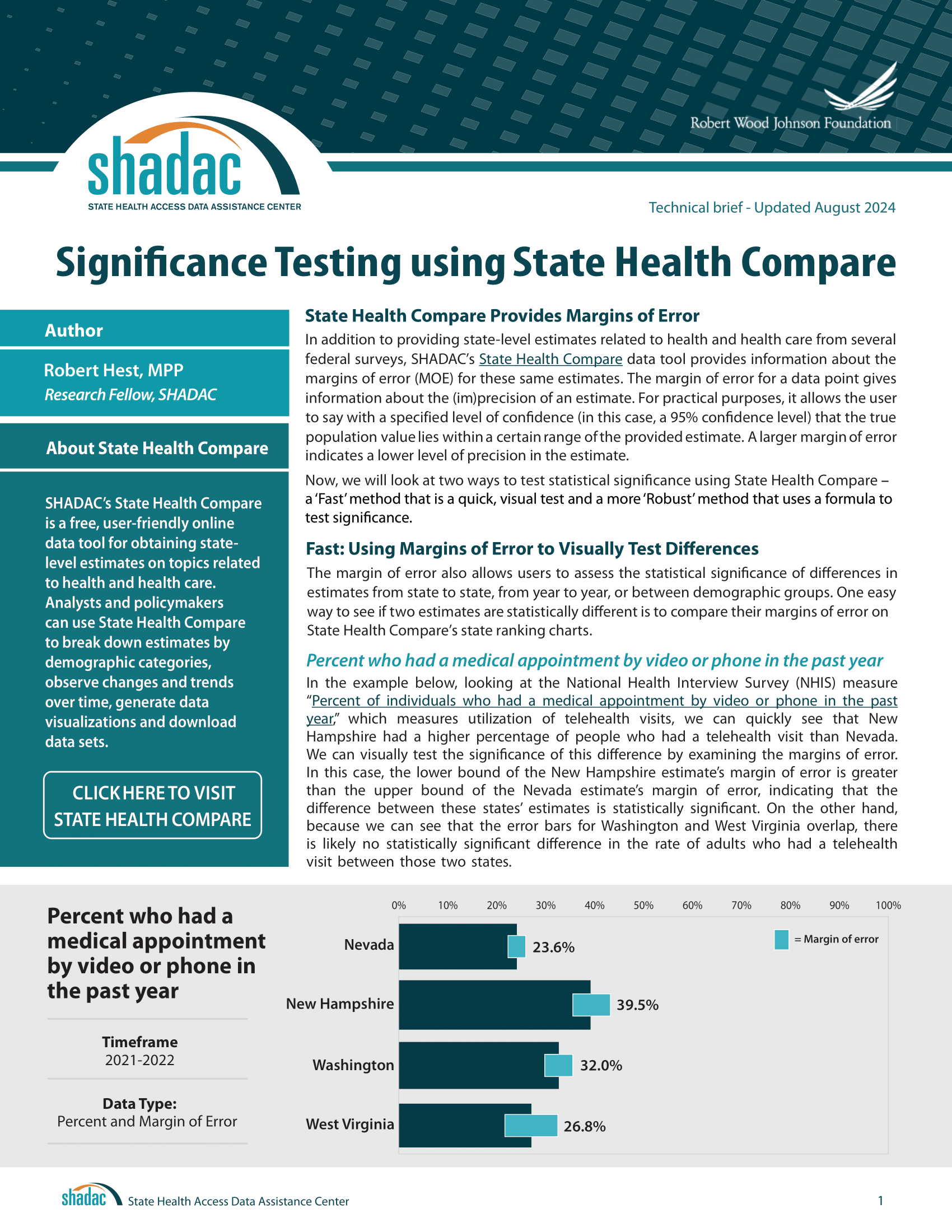
Now, let’s put all of those together. Using State Health Compare, let’s figure out whether the percentage of adults having a telehealth visit in Illinois in 2020-2021 and 2021-2022 are statistically significant from each other.
In 2020-2021, 31.28% of adults had a telehealth visit. In 2021-2022, 27.92% of adults had a telehealth visit.
Figure 1. Percent of Adults in Illinois Who Had a Telehealth Visit by Year
While we can see that a higher percentage of adults had a telehealth visit in 2020-2021 compared to 2021-2022, this doesn’t necessarily mean that the difference is statistically significant.
To find out if these percentages are statistically significant from each other, within a 95% confidence interval, we will conduct a t-test.
First, we will set our t-critical value, which corresponds to what confidence interval you are using. We will be using a 95% confidence interval, which corresponds to a t-critical value of 1.96.
The data from State Health Compare gives us the percentages for each state, as well as the margins of error (MOE). The MOE for 2020-2021 and 2021-2022 are 0.02021 & 0.02175, respectively.
Using the MOE, we can calculate the standard error (SE). To calculate the SE, divide the MOE by our t-critical value, 1.96.
SE for 2020-2021: 0.02021 / 1.96 = 0.01031
SE for 2021-2022: 0.02175 / 1.96 = 0.01109
We will need these numbers to calculate our t-statistic . However, before we can calculate the t-statistic, we need one more value: the difference in estimates.
This value is calculated by subtracting one estimate from the other. We will use the percentages of telehealth visits from each state.
Difference in Estimates of 2020-2021 & 2021-2022: 0.3128 – 0.2792 = 0.0336
Now, we have all the values needed to calculate our t-statistic, which is the ratio of the difference between the two estimates to the variability of the estimates. In other words, it answers: “How close to (or how far away from) ‘0’ is the difference, given the variability between the two estimates?”.
The t-statistic is calculated by plugging in the numbers from above into this formula:
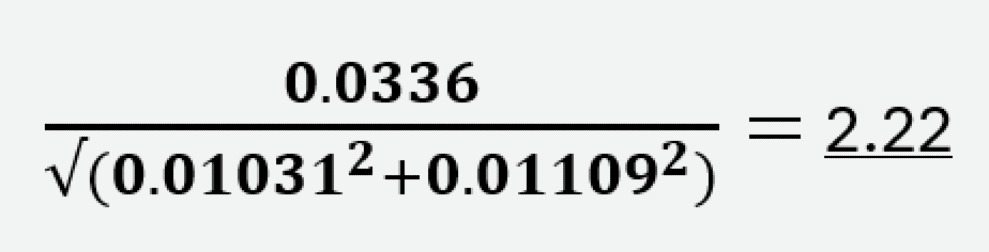
We can now compare this t-statistic to the t-critical value we determined above, which was 1.96. If the absolute value, which is the value of the number regardless of a positive or negative sign, of the t-statistic value is greater than the t-critical value, we can determine that the difference between the estimates is significant. If the absolute value of the t-statistic is less than the t-critical value, we cannot determine there is statistical significance.
Since 2.22 > 1.96, we can determine, with 95% certainty, that there was a significantly higher rate of telehealth visits in 2020-2021 in Illinois than in 2021-2022.
What This Means & Why It Matters
There are a number of reasons why statistical testing and significance are valuable for researchers and the field of research in general.
Statistical testing is important, as it allows researchers to draw conclusions from the presence or absence of statistical significance, prevents misinterpretation of results, and preserves the integrity of research.
Statistical significance is important because it tells researchers that the true difference between two population means is greater than zero. In other words, we can say with a specified level of confidence that, as a result of testing, two data points or estimates - or populations, in this particular case of assessing the number of adults who had telehealth visits between years – are different from one another.
However, a finding of statistical significance cannot tell us:
- That the difference is meaningful, just that it is different
- That the comparison makes sense analytically
- That the true difference is equal to the difference we observe
For more information on statistical testing and an example of how to determine significance when looking at estimates across different states, please read the accompanying brief at this link or by clicking on the image to the right.
If you’re interested in learning more about statistical analysis, data, and their intersection with health care & insurance coverage, check out some of SHADAC’s other blogs, like:
